The 70 years Theory of Games

博弈論七十年

博弈論由馮諾伊曼（John von Neumann）和摩根斯坦（Oskar Morgenstern）憑二人在1944年出版的巨著Theory of Games and Economic Behavior而奠定基礎，但是真正推動博弈論發展，令其大放異彩而廣受矚目的，當推以數學家納殊（John Nash）為首的少數後來者。他在1950年就合作博弈和非合作博弈發表的兩篇論文，今年適逢70周年，筆者且在這裏對博弈論作有選擇性的介紹，希望能對讀者有所啟發。

囚徒困境

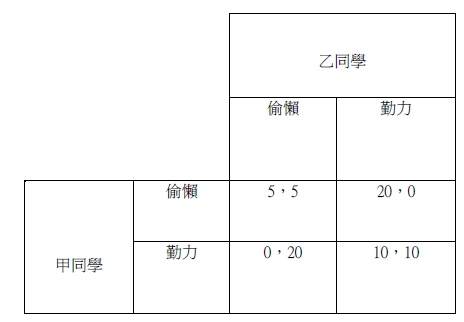
博弈論最家喻戶曉的例子，莫過於「囚徒困境」。舉例說，兩個同學要合作完成一個報告，他們各自可以選擇「勤力」或者「偷懶」，因此有四個可能的結果，對於每一個結果，他們都各有其收穫和成本。扣除成本，便計算到各自的淨利益，這裏且稱之為「盈利」（【表1】）。

表1顯示，從個人的盈利多寡考慮，甲同學覺得偷懶比勤力好，不管對方怎麼做；同樣考慮也適用於乙同學。結果出現了（偷懶，偷懶）這個雙輸的後果，然而（勤力，勤力）才是雙贏。這個例子說明了一個深刻的教訓：當每個人都把自己利益最大化的時候，整體結果可能是很差強人意的，即個人的理性可能導致集體的非理性。亞當斯密在他的《原富論》中，闡述了「無形之手」的概念，即每個人在追求自己的利益時，整體結果會令社會欣欣向榮。囚徒困境達到的結論，卻與之大相逕庭。

以上兩名同學合作所面對的的困惑，也可能出現在兩家公司，以至兩個國家之間。

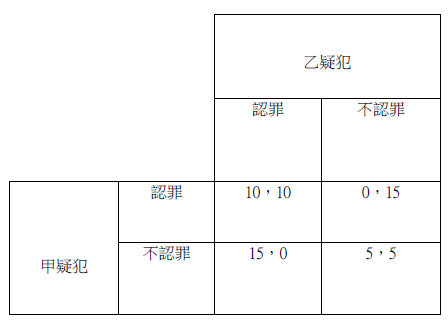
為什麼把這個處境稱為「囚徒困境」？原因很簡單，這個處境原本是以囚徒為例加以說明：兩名疑犯被捕之後，各自隔離審查，一方承認合謀犯罪，那麼不管對方認罪與否，都可以得到較輕的懲罰；弔詭的是，若雙方都不認罪才是雙贏（雙方的刑罰較輕）；若雙方都認罪，彼此的刑罰都較重，那是雙輸！【表2】

若無證據，也就無法知道這兩名被告的確是犯罪分子。表2所展示的，也可以是兩個無辜者面對一場冤案的困惑，各自為了自身（或家人）的安危，選擇承認自己沒有犯過的罪！這個版本最最能突顯這種困境的嚴重性。

怎樣解決囚徒困境？一個廣為討論的方法，是用長期合作來消弭短期機會主義行為，若能放遠目光，考慮到自己偷懶可能會被長期合作夥伴所嫌棄，自然不敢怠慢。

針對這類處境，最簡單的辦法是找一個可靠的合作拍檔。道德情操較高者能遵守諾言，要根據原則去處事，根本不是難事，有幸跟這類人合作，就不會出現囚徒困境。

不對稱均衡

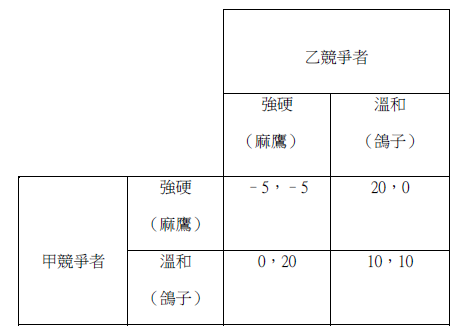
【表3】呈現另一場景，兩個生意對手遇到同一個機會，策略可軟（尋求合作）可硬（獨佔），其中有兩個不對稱的「納殊均衡」（Nash equilibrium），就是（強硬，溫和）和（溫和，強硬），即一方強硬的時候，另一方最優的反應是溫和；一方溫和時，另一方的最優反應是強硬。在兩個均衡之中，強硬一方收穫較高，就是俗語所謂「狹路相逢勇者勝」！

上述情況其實還有第三個均衡，就是雙方均採取混合策略，各以2/3的概率選擇強硬，1/3的概率選擇溫和。先從一方的角度分析，假如對方選擇強硬的概率是2/3，選擇溫和的概率是1/3，那麼一方若選擇強硬的策略，其預期收入將為2/3×（–5）＋1/3×20＝10/3，若選擇溫和的策略，其預期收入亦為2/3×0＋1/3×10＝10/3。對他而言，強硬或溫和都無所謂。第二方的考慮也一樣，因此，雙方用以上的概率選擇行為，就是一個均衡。

物種演化的博弈

這個博弈吸引了演化論生物學家的興趣，表3中的內容被賦予另一種解釋。表3中的兩個個體並不是人，而是兩隻飛禽，可能是麻鷹，也可能是鴿子，因此就有四個可能性。麻鷹天性強悍，鴿子則溫和。由於基因所限，鴿子遇到麻鷹會吃虧，收入有所不如，但若遇上另一鴿子，彼此禮讓和平，其盈利自會高於麻鷹遇到麻鷹時的情況。根據這個理解，表3嚴格來說並不是一個博弈，而是對四種可能性的說明，那兩隻飛禽並未有在不同策略之間做選擇。

我們可以合理假設，哪種飛禽盈利較高，其傳宗接代的能力也會較強，在飛禽中的比例就會上升，反之所佔比例就會下降。生物演化當然也會出現偶發的突變，麻鷹誕下小鴿子與鴿子誕下小鷹子，機率同樣微小，卻不等於零。

倘若飛禽中全都是麻鷹，那麼麻鷹每次覓食總會遇上同類惡鬥，其盈利反而不及那些突變產生的鴿子，鴿子就得以繁衍，在飛禽中的比例慢慢上升。同樣道理，倘若飛禽中全都是鴿子，鴿子的盈利，當然低於突變產生的麻鷹的盈利，因此麻鷹得以繁衍，其比例慢慢上升。

因此，雀鳥中全屬同類，都不是穩定的狀態。在一個長期的穩定狀態，兩種飛禽都會存在，雙方比例固定，各自的預期盈利相等，以致繁衍速度一樣。有趣的是，在這個長期穩定狀態中，麻鷹的比例剛好等於2/3，即等於第三個均衡算式中，每人使用強硬策略的概率！

上述兩種不同的處境，一是擁有自由意志的人類，一是單憑基因機械地行動的飛禽，但兩者之間又存在某種神秘的關係，實在值得我們深思。其實，人類的行為也往往毫無意識，純粹基於習慣，而習慣源於教育和生活環境；行為決定收入，收入又影響到人類的繁衍。

「破山中賊易，破心中賊難」

博弈論有助於研究個人的內心掙扎，譬如個人志願難以實行，往往因為抵受不住眼前誘惑等。若把內心掙扎理解為兩個利益不同的個體之間的衝突和互動，博弈論就大派用場，可藉以了解強制性退休金制度的利弊，或設計戒酒戒毒的方案等。

古希臘英雄奧德修斯在特洛伊戰爭之後和同伴乘船回希臘，途中來到一個有精靈出沒的海灣，其迷惑人的歌聲，足以令途經該處的船員遭遇滅頂之災。他於是把每個船員的耳朵塞住，不讓他們受到歌聲的迷惑。奧德修斯不僅塞住雙耳，還綁起雙手，以免抵受不住慾望而拿掉耳塞。

這個故事正反映出奧德修斯的內心掙扎好比一分為二的兩人博弈，其中憑理智採取的預防措施，終於克服易受誘惑的弱點，從而化解一劫。同一個人，其實內心往往有兩個「我」，在正常情況下的我，要經常保持覺醒，以免受另一個我支配。能以奧德修斯為榜樣，才可遠離許多麻煩。

納殊在1950年發表了那兩篇文章，博弈論自此取得長足發展，有助我們對經濟、政治、社會，自省的種種現象，作出系統的分析。從囚徒困境的概念可見，當每個人哪怕是用合法方式追求最大化的私利，整體後果卻可能極不理想。這種窘境可以通過建立長期關係克服；社會上法治精神和道德情操的提高，也有助防止囚徒困境的出現。麻鷹和鴿子的博弈反映教育和生活環境的結果，教育的重要性也就不言而喻。

明代理學大師王守仁就說過：「破山中賊易，破心中賊難。」要節制這個心中賊子，就要知道他的存在，以及其作息規律，須靠平日訓練有素，練就自省能力，更須避免目空一切，自以為是，免受制於另一個自我。

參考文獻

John F. Nash, Jr, “Equilibrium points in n-person games”, PNAS, 36（1）: pp. 48–49, 1950.

John F. Nash, Jr, “The Bargaining Problem”, Econometrica, 18（2）: pp. 155–162, 1950.

John von Neumann and Oskar Morgenstern, Theory of Games and Economic Behavior, Princeton University Press, 1944.

表1 兩名同學合作完成報告的囚徒困境